En la Parte 1, analizamos las probabilidades relativas de ataque y defensa en Risk, el juego de conquista mundial. Al final de la primera parte, concluimos que el ataque tenía un 47,15% de posibilidades de ganar la batalla para el primer soldado y nos preguntamos cómo los famosos conquistadores pudieron lograr sus hazañas en estas condiciones. Guardamos la discusión sobre el segundo soldado para la segunda parte.
Para refrescarnos la memoria, en Risk el ataque tira hasta 3 dados, mientras que la defensa tira hasta 2 dados. Se comparan las tiradas más altas de cada dado y el perdedor pierde un soldado, y la defensa gana en caso de empate. Luego se comparan las segundas tiradas más altas de cada dado y, una vez más, el perdedor pierde un soldado, y la defensa gana en caso de empate.
Bueno aquí estamos. Profundicemos.
(Aquí Y(Puede encontrar algún código donde confirmo las probabilidades a continuación).
Por supuesto, cuando se trata de las probabilidades del defensor, solo calculamos la tirada más baja, ya que solo tiene dos dados. Entonces, las probabilidades son un reflejo de las probabilidades que vimos con respecto a la tirada más alta. Esta vez hay 11 posibilidades dando una segunda tirada más alta de 1, 9 por 2, 7 por 3, etc. La probabilidad se puede calcular dividiendo el número total de posibles permutaciones de los dos dados de defensa por 36.
Calcular la segunda tirada más alta entre los tres dados del atacante difiere significativamente de los cálculos de la Parte 1. Seré honesto. Tuve un pequeño problema con esto. En los cálculos que siguen hay que tener en cuenta dos cosas.
- Debemos considerar tanto el número de resultados posibles Y de cuántas maneras puede ocurrir cada resultado. Por ejemplo, un resultado de (6, 2, 3) es, por supuesto, un resultado único, pero puede ocurrir de 6 maneras, correspondientes al dado en el que aparece cada valor. Puede ser uno de {(2, 3, 6), (2, 6, 3), (3, 2, 6), (3, 6, 2), (6, 2, 3), (6, 3). , 2)}. Por tanto, este resultado corresponde a 1*6 = 6 permutaciones. Para otro ejemplo, un resultado con Exactamente dos unos es en realidad una colección de 5 resultados, ya que el dado restante puede tomar cualquier valor entre 2 y 6. Y Esto puede suceder de 3 maneras, {(1, 1, x), (1, x, 1), (x, 1, 1)}, correspondiente a las 3 ubicaciones posibles para el dado restante, por lo que este resultado en realidad coincide en 5*3 = 15 permutaciones.
- Hay que tener cuidado con los dobles y triples. Estos deben considerarse por separado porque, si bien hay 6 formas de obtener un resultado (1, 2, 3), solo hay 3 formas de obtener un (1, 2, 2) y una única forma de obtener un (2, 2). , 2).
Teniendo en cuenta las consideraciones anteriores, estamos listos para continuar.
Considere la probabilidad de obtener un segundo resultado más alto de 1. Esto es relativamente simple. Está claro que la tirada más baja también es un 1. Por ahora, ignoraremos el caso en el que los 3 dados son 1. El dado más alto puede tomar cualquier valor entre 2 y 6, y puede aparecer en cualquiera de los 3 dados. , ya que no hemos especificado cuál de los 3 dados contiene la tirada más alta. Esto da un total de 3*5=15 permutaciones. Sumando el caso de un triple 1, obtenemos un total de 16 permutaciones. Mediante un argumento simétrico, podemos calcular que el mismo número de permutaciones da una segunda tirada más alta de 6.
Entonces, ¿qué tal un 2 como segundo resultado más alto? Por ahora, ignoraremos la posibilidad de múltiples dos y asumiremos que el resultado más alto fue mayor que 2 y el resultado más bajo fue menor que 2. El resultado más alto puede tomar 4 valores (3-6) y el resultado más bajo debe ser 1, para un total de 4 resultados, y estos pueden ocurrir en cualquiera de las 6 permutaciones de ubicaciones de los dados (3 posibilidades para la ubicación del resultado más alto (dado 1, dado 2 o dado 3) y las dos posibilidades restantes para la ubicación del resultado más bajo), para un total de 4*6=24 permutaciones. Ahora consideraremos los dobles dos, pero no los triples dos. Si hay exactamente 2 dos, entonces el dado restante puede tomar cualquiera de los 5 valores (excluyendo 2), y este dado restante puede ser cualquiera de los 3 dados, para 5*3= 15 permutaciones adicionales. Sumar el último caso del triple 2 da un total de 24+15+1 = 40 permutaciones. Un argumento paralelo da el mismo resultado para un segundo resultado más alto de 5.
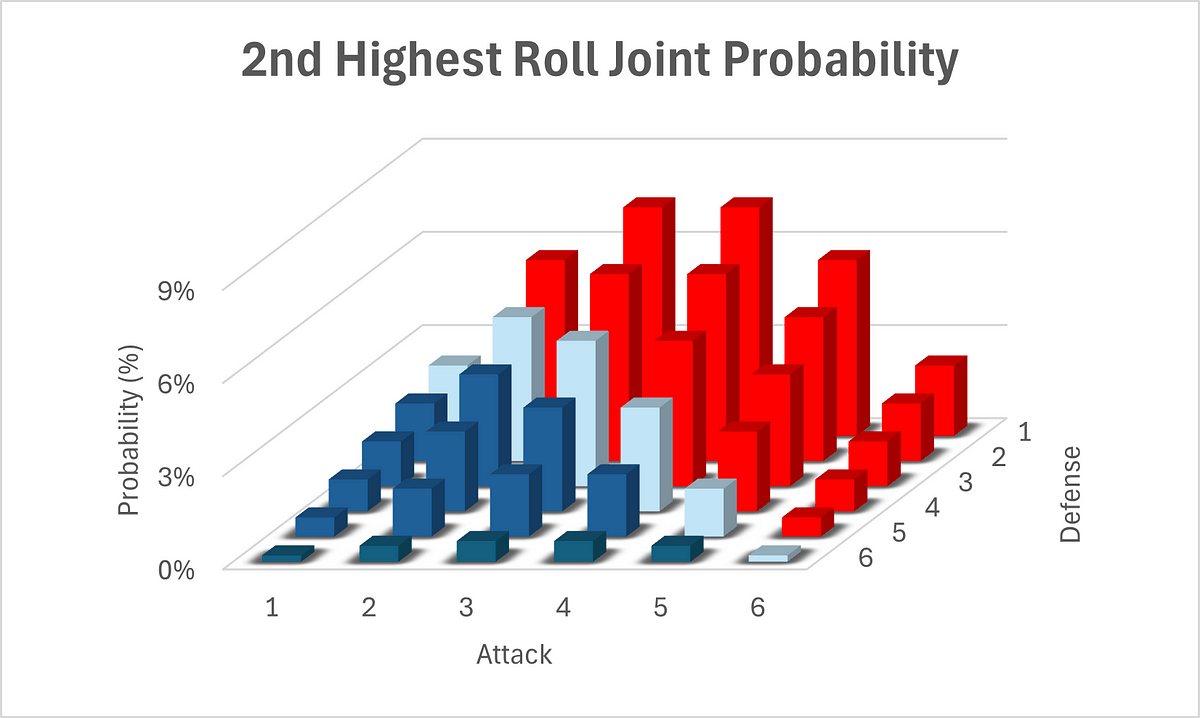
Finalmente, ¿qué tal 3 o 4? Comencemos con 3. Nuevamente, ignorando la posibilidad de múltiples tres, el resultado más alto puede tomar uno de los 3 valores (4, 5 o 6) y el resultado más bajo puede tomar uno de los 2 valores (1 o 2) , para un total de 6 resultados. Esto puede volver a suceder en cualquiera de las 6 permutaciones de dos dados, para un total de 6*6 = 36 permutaciones. En el caso de exactamente 2 treses, el otro dado podría tomar uno de 5 valores (cualquiera además de 3) y podría ocurrir en cualquiera de los tres dados, para un total de 5*3 = 15 permutaciones adicionales. Sumar la última posibilidad de 3 tres da un total de 36+15+1=52 permutaciones. Un cálculo paralelo también produce 52 permutaciones para un segundo resultado más alto de 4. Estos resultados se resumen en las imágenes siguientes.
Tenga en cuenta que las probabilidades de que se produzcan resultados de ataques son exactamente simétricas. Para ser matemáticamente preciso, P(x) = P(6-x). Volveremos a este punto.
Luego comparamos directamente las probabilidades de ataque y defensa.
Vemos que el ataque tiene aquí una ventaja significativa. Es mucho más probable obtener valores de 4, 5 o 6 que defensa.